概要
高分子の性質を理解するために必要な知識についてシリーズで解説しています。
今回は、高分子をセグメントが連結したモデルで考えた場合のサイズ(大きさ)について、まず、ポリスチレンにモデルを適用した結果を示した後、サイズの多様性を回転半径の分布として示します。
既に何度も示したように、高分子は図1のように幾つかのセグメントが連結した構造でモデル化されます。
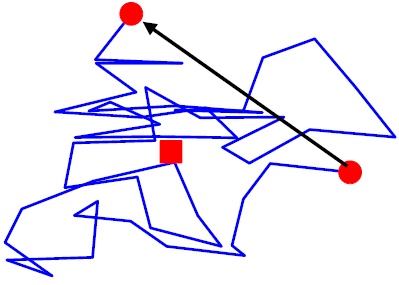
【図1】高分子のモデル
大きさ1のセグメントがn個(今の図では50個)連結した鎖を考える。
この図では3次元での鎖をX-Y平面に投影した図を示している。
●印:末端(始点と終点)、■印:重心、●印同士を結ぶ矢印:末端間距離
分子量300万程度のポリスチレンについて隣接するセグメントが同じ末端を1個共有することのみを条件としたモデルで表現した場合について示します。詳細は省略しますが、概ね6500個のセグメントが連結したモデルを考えることができます。このモデルで出現するコンフォメーションの1つについて、x-y平面、y-z平面、x-z平面への投影図を図2に示してみました。
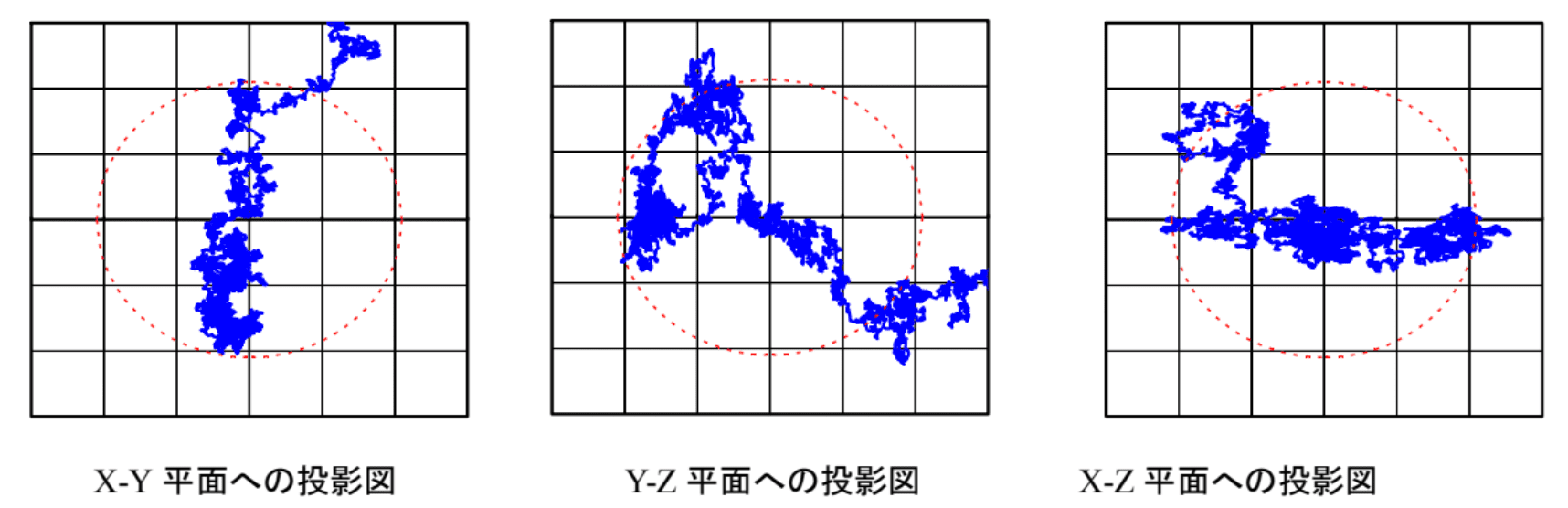
図2の青い実線が高分子の投影線で、赤い点線は重心を中心とした半径が回転半径Rgである球の表面の投影線です。球であれば、どの平面への投影図も円となるはずですが、青い線の投影図は、どの場合も円とはなっていません。楕円と表現した方が正確です。通常、高分子が球であることを仮定しますが、楕円体を考えた方が、より正確であることがわかります。しかし、1個のパラメーターで楕円体のサイズを正確に表現することはできません。そのため、質量の二次モーメント分布や流体力学的な効果が等価な球を考え、その半径をパラメーターにします。
このようなモデルに対して、セグメントが同じ数であっても、数多くのコンフォメーションが考えられます。そこで、6500個のセグメントが連結した高分子を考え、ランダムに1000個のコンフォメーションを発生させて、次の式
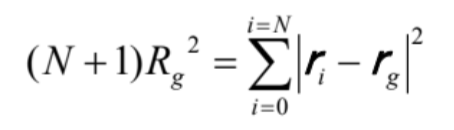 (1)
(1)
で計算したRgの分布を示したのが図3です。ここではセグメントの長さとして、アイソタクチックポリスチレンとシンジオタクチックポリスチレンの平均値3.58nmを使用して計算してあります。このとき、Rgの平均値は115nmとなります。隣接するセグメントが同じ末端を1個共有することのみを条件としたモデルで表現した場合、末端間距離はセグメントの数の0.5乗とセグメントの長さを乗じた値になることを用いて、(1)式からRgを計算して得られる値118nmに近いことがわかります。
図3をみると、回転半径の分布が結構広いことがわかります。このような分布が問題にされない点について、たとえば、サイズ排除クロマトグラフィーの検討の中でKreveldなどは、高分子の重心の拡散時間とセグメントの回転時間の比較から、重心が10 nm移動する間にセグメントは100回程度回転しているため、平均のRgでサイズ(大きさ)を記述できると主張しています3)。
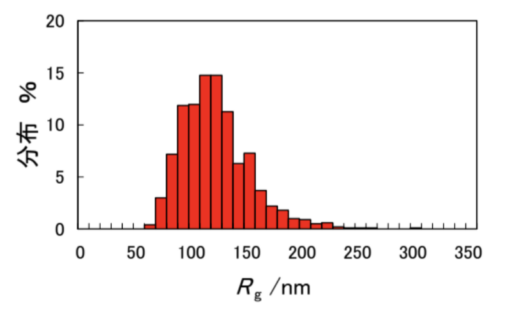
セグメント数6500の高分子を1000個発生させたときの回転半径の分布。ここではセグメントの長さを3.58nmとして計算してあります。
参考文献
| 1) | I.Teraoka, “Polymer Solutions”, JohnWiley, (2002) |
| 2) | H.Yamakawa, Ann.Rev.Phys.Chem., 35, 23 (1984) |
| 3) | M.E van Kreveld, N.van den Hoed, J.Chromatogr., 83, 111 (1973) |
